
MC Escher’s “Extra-logical Realities”: Artistic Progression From Architecture to Mathematics
Art
History
Europe
Written by Ana M. Carreño Leyva, Art courtesy of The M.C. Escher Company
Create a simple tessellation integrating techniques by Dutch artist M. C. Escher that relies on Islamic-inspired patterns.
The following activities and abridged text build off Escher +Alhambra = Infinity, written by Ana M. Carreño Leyva, and art courtesy of The M.C. Escher Company.
WARM UP
Scan the article’s photos and captions to predict its main idea.
IF YOU ONLY HAVE 15 MINUTES ...
Explain how Escher uses shapes, contrast and distortion to create optical illusions.
IF YOU ONLY HAVE 30 MINUTES ...
Demonstrate how specific artistic techniques added to Escher’s artistic appeal and longevity by analyzing his prints and visual elements.
VISUAL ANALYSIS
Use repeated abstract patterns to create a tessellation following Escher’s technique.
Escher + Alhambra = Infinity
Over 100 years ago, a 24-year-old artist from the Netherlands named Maurits Cornelius Escher sat down in a 14th-century meeting hall of the Alhambra palace in Granada, Spain. There he began to sketch the patterns of the tiles that filled its walls. His travel diary entry noted that he was so spellbound he spent the entire evening there copying an intricate, 16-point star mosaic, and that he did not stop until he had completed it with watercolors the next day. Later he reflected, “I became more and more intrigued by the fitting together of congruent figures.”
Fourteen years later, Escher and his wife, Guilietta, or Jetta, returned to Granada for three days in May 1936. He and Jetta both filled pages with notes and sketches. He marveled at how “the Moors were masters in the art of filling a plane with similar, interlocking figures.” The sketches from this trip inspired increasingly complex experiments with repetitive patterns of human- or animal-shaped figures. This was later extended into three dimensions through use of hyperbolic planes.

In 1936 he returned to the Alhambra and filled pages of his sketchbook with more patterns that informed his designs for the rest of his career. Referring to the interlocking symmetries of the patterns before him, he exclaimed in his journal, “How come no one has seen it before!”Rafael Pérez-Gómez, a professor of mathematics at the University of Granada and an expert on Escher, points out that despite Escher’s lack of formal training in mathematics or any field of science, he remains the artist most admired by mathematicians. Escher was fascinated by how the artisans of the Alhambra found solutions to representation that avoided empty spaces without using figurative images. At the same time, Pérez-Gómez says, they “convey(ed) the unity of divine presence in the universe, as well as its endlessness.”
This fascination with the regular division of a plane remained like a plant growing in his subconscious mind. Ultimately, it became his leading source of inspiration. He nurtured it by practicing, drawing, experimenting and experiencing—a process of pure persistence he carried on for decades. He played with combining and twisting parallelogram grids and interlocking polygons shaped as humans, lizards, fish, birds, frogs and monkeys. Simultaneously, Escher began to develop landscapes that integrated such figures into perspectives that were impossible from a rational, physical point of view. He also incorporated the Arab artisans use of contrasting color to enhance the symmetry of their designs.

Escher did not come to his passions in isolation. Escher was born in 1898 into a family of scientists. Escher struggled as a young student “with abstractions of numbers and letters”. He said, “my father and three of my brothers were all trained in the exact sciences or engineering, and I have always had an enormous respect for these things.” His brother Berend, a professor of geology, introduced him to crystallography. Escher enrolled in the Haarlem School for Architecture and Decorative Arts when he was 21. He enhanced his self-training by studying scientific articles on the regular division of the plane. He took inspiration from Hungarian mathematician George Pólya’s work, which categorized 17 flat periodic mosaics whose symmetries corresponded to the 17 Planar Crystallographic Groups.

Escher continued his artistic journey through the dynamic geometry of the plane. Escher saw an image that caught his attention in an article by Canadian mathematician Harold Scott Coxeter entitled, “Crystal Symmetry and Its Generalizations.” In 1954 a lifelong friendship blossomed when Escher met Coxeter in Amsterdam at the International Congress of Mathematicians. Pérez-Gómez explains that Escher learned to used French mathematician Henri Poincaré’s Euclidean model alongside the mentorship of Coxeter to make the regular division of the hyperbolic plane. The result was Escher’s Circle Limit series. For example, “Circle Limit IV,” is equivalent to the earlier, flat-plane pattern, “Angels and Devils,” but made on the model of the hyperbolic plane with right triangles with angles of 30 degrees, 45 degrees and 90 degrees. These triangles are only possible in hyperbolic geometry, since their angles add up to less than 180 degrees. “It is more than surprising to think that its origin is in the tiled mosaic of the Alhambra,” as is one of Escher’s best-known images, “Day and Night,” says Pérez-Gómez.
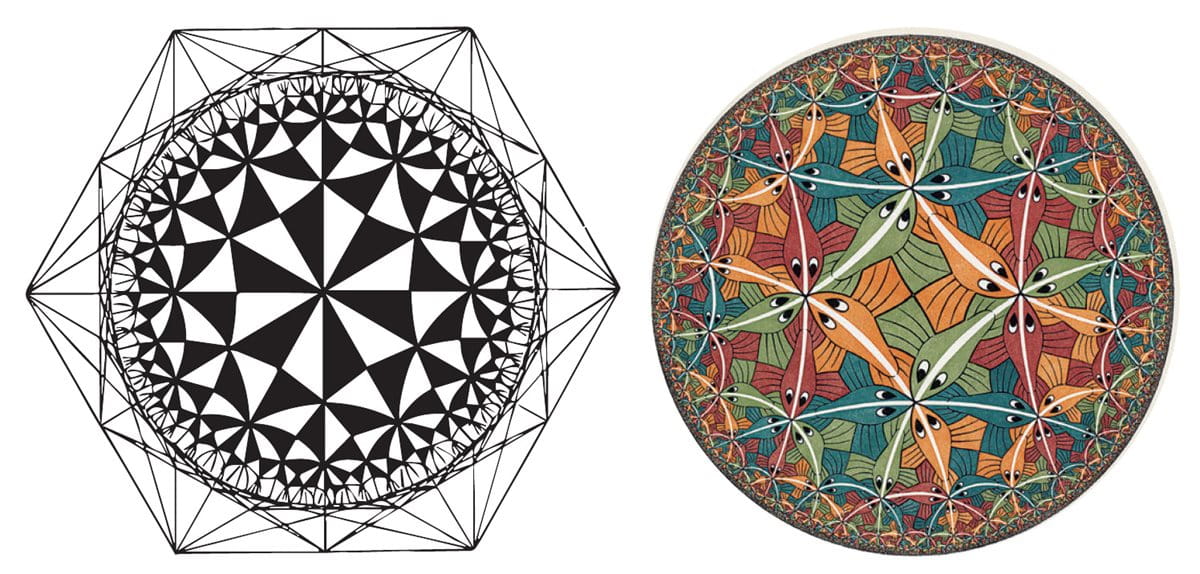
What makes Escher’s “extra-logical realities” so compelling? Perhaps it is the search for balance within the duality of infinity versus limited space. Maybe this concept is enhanced through black-and-white dichotomies? Is it symmetry amid rhythmic repetitions and color combinations that made figurative shapes appear kinetic and vibrant? All were strategies to the contrary that were simultaneously complementary. Escher also added potential for infinity just outside our perception of the physical world. He kept them in balance by using the same proportions of colors. This ensured that one did not overpower another but allowed each to boost the others. By playing with space and time, he suggests the ways reality may surpass our senses. His medium was not in the humanities but in the abstract language of mathematics. He used paradoxes to offer up spatial mysteries.

From his early interests in patterns to his systematic study of Moorish architecture, he took crystallographic geometry toward spatial infinity. Later, through hyperbolic planes, he pushed practical geometry into the fourth dimension of time. This put his works well within the framework of 20th-century European vanguardist art movements such as Dadaism, Surrealism and Op Art. His drawings have been endlessly reproduced in popular culture, from vinyl LP covers to wall posters and fabric designs.

Escher’s works invite our eyes to travel never-ending landscapes. They offer the opportunity to walk spaces with no beginnings and no ends, where horizons fold into foregrounds. Within his work, we are left awestruck by seemingly impossible complexity.
Question: In what ways did Escher’s travels influence the concepts and styles that embodied his artwork?
Escher was intrigued by the patterns at the Alhambra Palace in Granada, Spain and repeatedly drew them for years in his art notebooks.
Question: How was Escher’s educational training different than that of his family?
Escher’s father and three of his brothers studied and sought employment in the fields of mathematics and science, while Escher attended the Haarlem School for Architecture and Decorative Arts.
Question: How does Escher’s artwork provide visual metaphors for abstract concepts such as math and science?
Escher’s artwork provides concrete representations of the concepts of infinity, paradoxes, duality, symmetry and the hyperbolic plane among many others.
Other lessons

The Gambia’s Groundnuts: Identifying Problems and Solutions
Environmental Studies
Anthropology
West Africa
Identify the challenges facing growers of the Gambia’s most-important product—the peanut.
The Past Is Told by the Victors: Exploring the Other Side of History
Art
History
Fertile Crescent
Explore how history’s narrative is dictated by the victors and its affect on our understanding of it.
How Art Connects
For the Teacher's Desk
Art links everything—cultures, history, even math. Want to hook students? Try teaching through the art that surrounds us with these stories.